Chapter 2 (p.50) – Solutions - #2                                         p.1

 

21. “Firing down the barrel of a rife” – With ‘barrel of the rifle’ problems, we’re usually given , the length of the barrel (or runway or how far the crossbow is pulled back, etc.).

We always start from rest so v0 = 0 m/s. They either give the final velocity (muzzle speed)  or they give the acceleration and ask for the other, so we use kinematics equation #3:

(a) (memorize the ‘box’) .

(b) What do ‘they’ mean by compare this with g = 9.8 m/s2 ? Express the acceleration ‘in terms’ of g. Divide by 9.8 and write as: 27,900g (not grams!). Air Force pilots can blackout at accelerations of anywhere from 4 to 6 g’s.

Fighter Pilots and Blackout: http://ryono.net/apphysics/blackout.html

 

22. “Stopping Time” – Well, this is sort of a backwards stopping time problem. It’s like firing a bullet down the barrel of a gun, but instead of being given , we get

We always (well, this problem is backward so…) come to a stop so we have  = 0 m/s. We’re usually given the initial velocity and acceleration and asked for stopping time.

Anyway… in this problem, we are given  and a time of 8 sec.

We’re asked for the acceleration. (Even if acceleration is not constant, we can still calculate the average acceleration using: .)

Anyway… ‘Stopping time problems’ are always solved using kinematics equation #2:

(a) (memorize the ‘box’)

(b) To find distances, we most often use equation #3:

(c) Using equation #2 again, we can find instantaneous velocity:  

 

23. Now we can’t directly use equation #2 or #3. ??? We’re given and . Hmm…

(a) We’ll use the definition of average velocity:  or d=rt: 40 = r(2.8)

and the Merton Rule: .

(b) Now, we can use either eq. #2 or #3. I like #2:  2.8 = a(8.5) + 6.62 

Did you ‘catch’ that “smoothly slowing down” phrase? What’s meant by that?

This means no jerks! Acceleration is constant. A jerk is actually a physics term.

It’s the derivative of acceleration w.r.t. time (the 3rd derivative of the position function…)

Since a = -.448 (constant), da/dt = 0 m/s3. If acceleration is constant (smoothly changing velocity), then the associated force is constant so dF/dt = 0 and Mass X Jerk = Yank. !!!

I thought you might like to know that!

 

                                                Chapter 2 (p.50) – Solutions - 2                                   p.2

 

24. I don’t like this kind of problem because not only are we using American units, but we’re mixing miles with feet. So why, you ask, did I assign this? We’re in America so we’d better practice with American units and unit conversions! Sorry!

‘Stopping Distance Problem’ – Use equation #3: We could convert to SI units (inside the back cover of our text is a great unit conversion page with a bonus Greek alphabet!)

02 = 352 + 2a(40)

Then at 70 mph, we have: 02 = 702 + 2(-15.3) .

Hmm… double your speed and your stopping distance is 4 times a long… We’ll see this…

Let’s try this problem as an AP problem. Given a constant acceleration, a, and an initial velocity, vi , we obtain a stopping distance of d1. Find the stopping distance (d2) in terms of d1 if we double our initial velocity to ‘2vi’.

02 = vi2 + 2ad1 or d1=vi2/2a, so for the same ‘a’ but with an initial velocity of ‘2vi’, we get:

02 = (2vi)2 + 2ad2 which gives us: d2 = 4(vi2/2a) = 4d1 Q.E.D.

So if d­1 = 40 ft or meters or miles… d2 = 4(40) = 160 ft or meters or miles! No units!

 

25. Okay, centimeters are metric, but they’re not SI (or MKS) units! Let’s convert to SI.

We’re given xi = .03m, xf = -.05m, t = 2sec, vi = .12m/s and constant acceleration.

Let’s use equation #1:  (oh yeah, memorize the ‘box’!)

 

26. (See graph on p.52)

(a) Displacement (in this case, ) is area under the curve or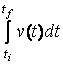

Method A – Counting Boxes – There are 24 boxes (including partial boxes) but only 12 full boxes.  Count the remaining 12 partial boxes as ‘half-boxes’ (ie, divide by 2) and we get 12/2 = 6 more boxes. Total boxes = 12 + 6 = 18 (Watch out for the units on the box sides!) Each box is 10 X 10 = 100 m in ‘area’. So d = 1800 m.  (Hmm, the book’s answer was 1870 m. This was an easy method, but that averaging assumed a random shape to the graph and the graph is ‘hugging’ some lines, so…)

 

Method B – Counting boxes and fitting partial boxes together… Okay, that first method was fun, but let’s try matching pieces together. Okay, I got 19 boxes, so 19(100) = 1900 m.

(I must confess, I numbered the boxes, so I wouldn’t double count them! Okay, just this once, you can number them also. Don’t bother to erase. I think it will be instructive for the next student. This is a one-time thing. Never again will I write in a text book…)

 

 

                                                Chapter 2 (p.50) – Solutions -2                                     p.3

27. Ah, a nice easy calculus problem.

(a) At the turnaround point, v = 0, so we took the derivative of x… and set it equal to zero.

. Now we plug that time into the x-function to get:

(b) When a object is thrown upward with a velocity of 1.732 m/s, what is it’s velocity as it passes the original position (on the way down)? Correcto! -1.732 m/s (George Washington)

Since we can ‘read’ the initial velocity as 3 m/s from the x-equation above, vf = -3 m/s.

Proof? Let’s use kinematic equation #3:  and realizing that = 0 here, we get vf2 = vi2 + 0, which means that the speeds are the same, . The directions are opposite, so we have vf = -vi. QED

 

28. The problems are getting easier!

(a) Given time (2.5 sec), we’ll use equation #2: v = 3(2.5) + 5.2 = 12.7 m/s

(b) Same time, different acceleration: v = -3(2.5) + 5.2 = -2.3 m/s

 

29. A tricky ‘black’ problem. I started with (b) because I was thinking stopping distance!

(b) Equation #3: vf2 = 02 + 2(10)(400) gives us vf =  (full credit for )

(a) Now we can use equation #2: 89.4 = 10t + 0 which gives us t = 8.94 sec or sec.

 

30. (a) Equation #1 (the position function):

           Equation #2 (the velocity function):   (or just take the derivative, dx/dt)

       (b) Equation #3 (stopping distance):  

 

31. (a) Stopping Time Problem – Equation #2: 0 = -5t + 100 or t =

(b) Stopping Distance Problem – Equation #3: 02 = 1002 + 2(-5) 

 

32. This problem is even harder than #23 above where we couldn’t use equations #2 and #3 directly. We’re given time (4.2 sec) and displacement (62.4 m) and even acceleration (-5.6 m/s2). But no vi or vf ??? Let’s see… What equation(s) can we use?

Equation #1 has both time and displacement in it (if we move x0 over to the left side…)

Now we can use either equation #2 or #3. I like #2: vf = (-5.6)(4.2) + 25.5 =

33. Do problem #32 with one formula! . Now use eq. #2

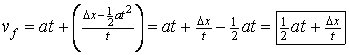  #32?